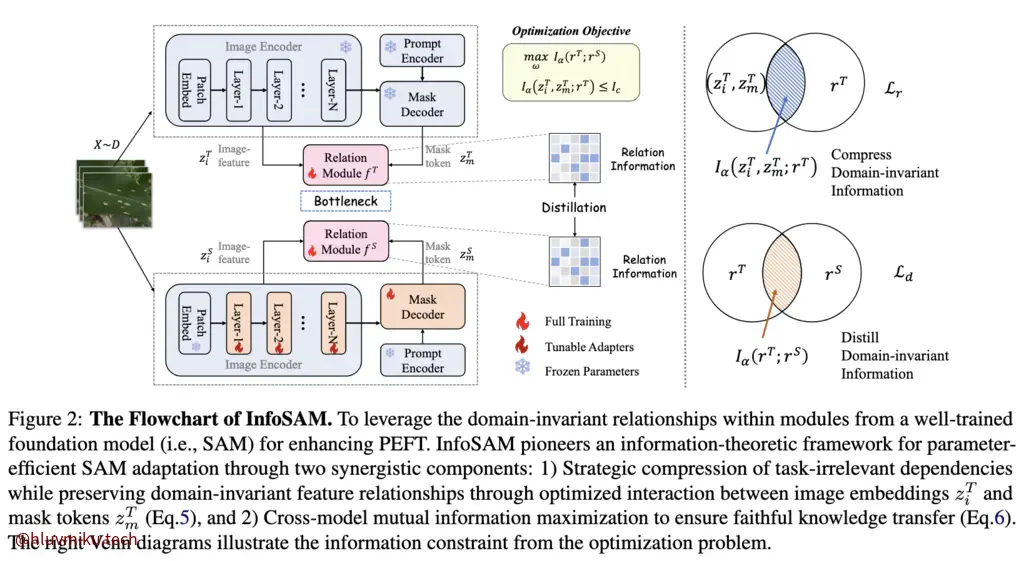
论文简读：《InfoSAM: Fine-Tuning the Segment Anything Model from An Information-Theoretic Perspective》

【PDF:InfoSAM Fine-Tuning the Segment Anything Model from An Information-Theoretic Perspective.pdf】

这篇文章设计的结构很简单，亮点在于loss设计以及可解释性上。

概要

However, existing PEFT methods for SAM neglect the domain-invariant relations encoded in the pretrained model.

文章认为，现有的PEFT后训练微调会忽视一些模型内嵌的领域不变关系，直接训练可能造成冗余或者破坏现有内在关系。于是本文从信息论角度来进行蒸馏+微调，通过巧妙设计Loss和Relation Module设计让模型学到领域不变关系。

Introduction

We argue that this is because task-specific tuning tends to override or suppress the universal visual features learned during pre-training.

直接进行特定任务的微调会导致原有的视觉特征被覆盖或者抑制。

为了更有效的进行PEFT，文章着重于解决以下两点：

How can we extract the domain-invariant relationship from pretrained foundation models?

How can we effectively transfer the extracted information to fine-tuned models?

对于问题1，文章设计了一个Relation module从Pretrained SAM来提取关键pattern，通过最小化Image Encoder、Mask Decoder与Relation Module的互信息来有效提取领域不变关系。简单来说，Relation Module 不应该记住 task-specific feature，而应该聚焦于稳定、低熵、可复用的关系结构。而对于问题2，文章巧妙设计了一个蒸馏结构，同时最大化Teacher和Student的互信息以有效transfer提取到的信息。在这里，文章主要用到了 Re ́nyi’s entropy-based quantification from information theory。

Renyi-alpha Entropy

Re ́nyi’s entropy定义如下：

\mathbf{S}_\alpha = \frac{1}{1-\alpha}\log_2[\Sigma_{i=1}^n\lambda_i^\alpha(\mathbf{A})]

其中

\mathbf{A}_{ij} = \frac{1}{n}\frac{K_{ij}}{\sqrt{K_{ii}K_{jj}}}

是归一化后的核矩阵。

在文中，我们采用了Renyi-2 Entropy，这时，我们可以简单地使用 ||\mathbf{A}||F^2来替换 \Sigma{i=1}^n\lambda_i^2(\mathbf{A})。对于核函数，文章采用了最简单的线性核：直接转置点积的方法。这个Renyi-alpha Entropy可以用来衡量“不变与变化”。

Methodology

Compressing Intra-SAM Relations

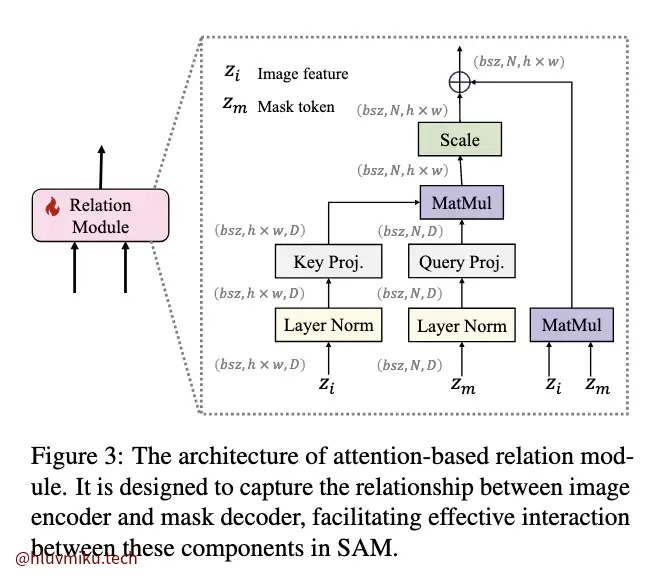
Relation Module设计很简单，是一个类似Attn的结构。真正巧妙之处在于它设计的loss:

\mathcal{L}_r = -\log_2(||G_r^T||_F^2)-(-\log_2(||G_{imr}^T||_F^2))

简要来说前面一项从信息论视角看是正则项，用于约束关系模块。第二项则希望ImageEncoder、MaskDecoder、RelationModule之间的互信息尽可能的小。注意到这个Loss是对Teacher而言的，而Teacher中只有RelationModule可被训练，这就迫使RelationModule提取**“不变特征”**。

Maximizing Inter-SAM Relations

接下来我们来看看蒸馏。

While most existing works (Ahn et al., 2019; Kuang et al., 2023) focus on minimizing a lower bound of mutual information, we directly maximize the matrix-based R ́enyi’s mutual information itself to avoid the expensive evaluation of underlying distribution for distillation loss.

简要来说，本文直接最大化两个特征模块提取结果的互信息，而不是优化互信息的下界。做法也很简单：

\mathcal{L}_{d}=-(-\log_2(||G_{imr}^T||_F^2)-\log_2(||G_{imr}^S||_F^2)+\log_2(||G_{imr}^TS||_F^2))

最后将这俩loss再加上一个CElos作为最终的loss。

实现细节

在阅读论文时，我有几个疑惑：student的RelationModule是如何训练的，核函数是如何选择的？作者提供的伪代码都给了解答：student和teacher共用一个RelationModule，用的是最简单的线性核

# F_t, F_s: Pre-trained SAM (teacher) and fine-tuned SAM (student)
# z_t_i, z_s_i: The output of the teacher and student image encoders
# z_t_m, z_s_m: The output tokens in mask decoder of the teacher and student
# f_t, f_s: Teacher and student relation modules
# y_t, y_s: Teacher and student outputs
# y: Ground-truth labels
# Frob: Function for computing the square of the Frobenius norm

for x, y in loader:
    # Forward pass
    z_t_i, z_t_m, y_t = F_t(x)
    z_s_i, z_s_m, y_s = F_s(x)

    # Compute structure loss
    loss_ce = struct_loss(y_s, y)

    # Compute relations between image encoder and mask decoder
    f_s = f_t
    r_t = f_t(z_t_i, z_t_m)
    r_s = f_t(z_s_i, z_s_m)

    # Normalize the representations
    z_t_i_norm = F.normalize(z_t_i, p=2)
    z_t_m_norm = F.normalize(z_t_m, p=2)

    # Compute normalized Gram matrices for compression loss_r
    G_t_i = matmul(z_t_i_norm, z_t_i_norm.T)
    G_t_m = matmul(z_t_m_norm, z_t_m_norm.T)
    G_t_f = matmul(r_t, r_t.T)
    G_t_f_norm = G_t_f / trace(G_t_f)
    G_t_imr_norm = G_t_i * G_t_m * G_t_f / trace(G_t_i * G_t_m * G_t_f)

    # Compute normalized Gram matrices for distillation loss_d
    G_s_f = matmul(r_s, r_s.T)
    G_s_f_norm = G_s_f / trace(G_s_f)
    G_ts_f_norm = G_s_f * G_t_f / trace(G_s_f * G_t_f)

    # Compute relation compression loss_r and distillation loss_d
    loss_r = - log2(Frob(G_t_f_norm)) + log2(Frob(G_t_imr_norm))
    loss_d = log2(Frob(G_t_f_norm)) + log2(Frob(G_s_f_norm)) - log2(Frob(G_ts_f_norm))
    loss_info = lamda_1 * loss_r + lamda_2 * loss_d

    # The overall loss
    loss = loss_ce + loss_info

    # Optimization step
    loss.backward()
    optimizer.step()

总结

这篇文章看得我汗流浃背——学了一学期的信息论感觉完全白学了。由于是简读，核函数、Ahn et al., 2019;、Kuang et al., 2023还有些其他的东西都没详细展开，相关论文也没咋读。但这篇文章确实非常精彩，无论是从工程角度还是学术角度。